A Correlation Coefficient Can Range in Value From
The 'correlation coefficient' was coined past Karl Pearson in 1896. Accordingly, this statistic is over a century quondam, and is nevertheless going stiff. It is one of the most used statistics today, second to the mean. The correlation coefficient's weaknesses and warnings of misuse are well documented. As a fifteen-twelvemonth practiced consulting statistician, who also teaches statisticians standing and professional studies for the Database Marketing/Information Mining Industry, I see besides often that the weaknesses and warnings are not heeded. Among the weaknesses, I have never seen the issue that the correlation coefficient interval [−1, +1] is restricted by the individual distributions of the two variables beingness correlated. The purpose of this commodity is (1) to introduce the effects the distributions of the two individual variables have on the correlation coefficient interval and (2) to provide a procedure for computing an adjusted correlation coefficient, whose realised correlation coefficient interval is often shorter than the original one.
The implication for marketers is that now they have the adjusted correlation coefficient every bit a more than reliable measure of the important 'central-drivers' of their marketing models. In turn, this allows the marketers to develop more constructive targeted marketing strategies for their campaigns.
CORRELATION COEFFICIENT BASICS
The correlation coefficient, denoted by r, is a mensurate of the force of the straight-line or linear human relationship between ii variables. The well-known correlation coefficient is often misused, because its linearity assumption is not tested. The correlation coefficient can – by definition, that is, theoretically – assume any value in the interval between +1 and −1, including the terminate values +ane or −one.
The following points are the accepted guidelines for interpreting the correlation coefficient:
- 1
0 indicates no linear human relationship.
- 2
+ane indicates a perfect positive linear human relationship – as 1 variable increases in its values, the other variable also increases in its values through an exact linear rule.
- iii
−1 indicates a perfect negative linear relationship – as ane variable increases in its values, the other variable decreases in its values through an exact linear rule.
- 4
Values betwixt 0 and 0.3 (0 and −0.three) indicate a weak positive (negative) linear relationship through a shaky linear rule.
- v
Values between 0.3 and 0.7 (0.3 and −0.7) indicate a moderate positive (negative) linear human relationship through a fuzzy-firm linear rule.
- half dozen
Values between 0.vii and one.0 (−0.7 and −1.0) betoken a stiff positive (negative) linear relationship through a firm linear rule.
- 7
The value of r 2 , called the coefficient of determination, and denoted R 2 is typically interpreted every bit 'the pct of variation in 1 variable explained by the other variable,' or 'the percentage of variation shared betwixt the two variables.' Proficient things to know about R ii :
- a)
It is the correlation coefficient between the observed and modelled (predicted) information values.
- b)
It can increment as the number of predictor variables in the model increases; it does not decrease. Modellers unwittingly may call up that a 'improve' model is being built, equally s/he has a tendency to include more (unnecessary) predictor variables in the model. Accordingly, an adjustment of R two was developed, accordingly called adjusted R 2 . The explanation of this statistic is the aforementioned as R 2 , but it penalises the statistic when unnecessary variables are included in the model.
- c)
Specifically, the adjusted R 2 adjusts the R 2 for the sample size and the number of variables in the regression model. Therefore, the adjusted R 2 allows for an 'apples-to-apples' comparing betwixt models with different numbers of variables and different sample sizes. Unlike R two , the adjusted R 2 does non necessarily increase, if a predictor variable is added to a model.
- d)
It is a showtime-chroma indicator of a good model.
- e)
It is oft misused equally the measure to assess which model produces improve predictions. The RMSE (root mean squared error) is the mensurate for determining the better model. The smaller the RMSE value, the ameliorate the model, viz., the more precise the predictions.
- a)
- eight
Linearity Assumption: the correlation coefficient requires that the underlying relationship between the two variables nether consideration is linear. If the relationship is known to be linear, or the observed blueprint between the ii variables appears to be linear, so the correlation coefficient provides a reliable measure of the strength of the linear human relationship. If the relationship is known to exist not-linear, or the observed design appears to be non-linear, then the correlation coefficient is not useful, or at to the lowest degree questionable.
Adding OF THE CORRELATION COEFFICIENT
The adding of the correlation coefficient for two variables, say Ten and Y, is simple to understand. Permit zX and zY be the standardised versions of X and Y, respectively, that is, zX and zY are both re-expressed to have means equal to 0 and standard deviations (s.d.) equal to i. The re-expressions used to obtain the standardised scores are in equations (1) and (2):

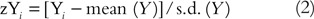
The correlation coefficient is defined equally the mean production of the paired standardised scores (zX i , zY i ) every bit expressed in equation (3).
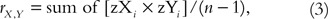
Where n is the sample size.
For a simple illustration of the calculation, consider the sample of five observations in Table 1. Columns zX and zY incorporate the standardised scores of X and Y, respectively. The final column is the product of the paired standardised scores. The sum of these scores is ane.83. The mean of these scores (using the adjusted divisor northward–1, not due north) is 0.46. Thus, r X,Y =0.46.
REMATCHING
Equally mentioned higher up, the correlation coefficient theoretically assumes values in the interval betwixt +1 and −one, including the end values +1 or −one (an interval that includes the end values is called a airtight interval, and is denoted with left and right square brackets: [, and], respectively. Accordingly, the correlation coefficient assumes values in the airtight interval [−1, +1]). However, it is not well known that the correlation coefficient airtight interval is restricted by the shapes (distributions) of the individual 10 data and the private Y data. The extent to which the shapes of the private X and private Y data differ affects the length of the realised correlation coefficient closed interval, which is often shorter than the theoretical interval. Clearly, a shorter realised correlation coefficient closed interval necessitates the calculation of the adjusted correlation coefficient (to be discussed below).
The length of the realised correlation coefficient airtight interval is determined by the process of 'rematching'. Rematching takes the original (10, Y) paired data to create new (Ten, Y) 'rematched-paired' data such that all the rematched-paired data produce the strongest positive and strongest negative relationships. The correlation coefficients of the strongest positive and strongest negative relationships yield the length of the realised correlation coefficient closed interval. The rematching process is as follows:
- 1
The strongest positive relationship comes about when the highest X-value is paired with the highest Y-value; the second highest X-value is paired with the 2nd highest Y-value, and and so on until the lowest Ten-value is paired with the everyman Y-value.
- 2
The strongest negative relationship comes about when the highest, say, X-value is paired with the everyman Y-value; the second highest Ten-value is paired with the 2nd everyman Y-value, and then on until the highest X-value is paired with the everyman Y-value.
Continuing with the data in Table ane, I rematch the X, Y information in Table 2. The rematching produces:

So, just as there is an aligning for R 2 , in that location is an aligning for the correlation coefficient due to the individual shapes of the X and Y information. Thus, the restricted, realised correlation coefficient closed interval is [−0.99, +0.90], and the adjusted correlation coefficient tin can now exist calculated.
CALCULATION OF THE Adjusted CORRELATION COEFFICIENT
The adjusted correlation coefficient is obtained by dividing the original correlation coefficient by the rematched correlation coefficient, whose sign is that of the sign of original correlation coefficient. The sign of adjusted correlation coefficient is the sign of original correlation coefficient. If the sign of the original r is negative, and so the sign of the adapted r is negative, fifty-fifty though the arithmetic of dividing two negative numbers yields a positive number. The expression in (4) provides simply the numerical value of the adjusted correlation coefficient. In this example, the adapted correlation coefficient between X and Y is defined in expression (4): the original correlation coefficient with a positive sign is divided by the positive-rematched original correlation.
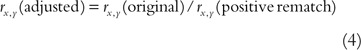
Thus, r X,Y (adjusted)=0.51 (=0.46/0.xc), a ten.9 per cent increase over the original correlation coefficient.
IMPLICATION OF REMATCHING
The correlation coefficient is restricted by the observed shapes of the individual X- and Y-values. The shape of the data has the following effects:
- one
Regardless of the shape of either variable, symmetric or otherwise, if i variable'southward shape is unlike than the other variable's shape, the correlation coefficient is restricted.
- ii
The restriction is indicated by the rematch.
- iii
It is non possible to obtain perfect correlation unless the variables have the same shape, symmetric or otherwise.
- 4
A status that is necessary for a perfect correlation is that the shapes must be the same, but information technology does not guarantee a perfect correlation.
CONCLUSION
The everyday correlation coefficient is still going potent after its introduction over 100 years. The statistic is well studied and its weakness and warnings of misuse, unfortunately, at least for this writer, have not been heeded. I discuss a 'possibly' unknown restriction on the values that the correlation coefficient assumes, namely, the observed values fall within a shorter than the always taught [−ane, +1] interval. I innovate the effects of the individual distributions of the two variables on the correlation coefficient closed interval, and provide a procedure for calculating an adapted correlation coefficient, whose realised correlation coefficient airtight interval is frequently shorter than the original one, which reflects a more than precise measure of linear relationship betwixt the two variables nether study.
The implication for marketers is that at present they have the adjusted correlation coefficient, every bit a more reliable measure of the important 'central drivers' of their marketing models. In plough, this allows the marketers to develop more than constructive targeted marketing strategies for their campaigns.
Author information
Affiliations
Corresponding author
Additional data
1founder and President of DM STAT-ane Consulting, has made the company the ensample for Statistical Modeling & Assay and Data Mining in Straight & Database Marketing, Client Human relationship Management, Business Intelligence and It. DM STAT-1 specialises in the full range of standard statistical techniques, and methods using hybrid car learning-statistics algorithms, such as its patented GenlQ Model© Modeling & Data Mining Software, to attain its Clients' Goals across industries of Banking, Insurance, Finance, Retail, Telecommunications, Healthcare, Pharmaceutical, Publication & Circulation, Mass & Direct Advertizement, Catalog Marketing, eastward-Commerce, Spider web-mining, B2B, Man Upper-case letter Management and Risk Direction. Bruce'south par excellence consulting expertise is clearly apparent, as he is the author of the acknowledged volume Statistical Modeling and Assay for Database Marketing: Effective Techniques for Mining Big Data (based on Amazon Sales Rank since June 2003), and assures: the client's marketing determination problems volition be solved with the optimal problem-solution methodology; rapid outset-up and timely delivery of projects results; and, the client's projects will be executed with the highest level of statistical do. He is often-invited speaker at public and private industry events.
Rights and permissions
About this article
Cite this article
Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they?. J Target Meas Anal Marker 17, 139–142 (2009). https://doi.org/10.1057/jt.2009.5
-
Published:
-
Issue Engagement:
-
DOI : https://doi.org/10.1057/jt.2009.5
Source: https://link.springer.com/article/10.1057/jt.2009.5
0 Response to "A Correlation Coefficient Can Range in Value From"
Post a Comment