What name is given to the 0* latitude line?

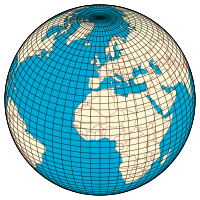
Geographic coordinate specifying north–south position

A graticule on the Earth as a sphere or an ellipsoid. The lines from pole to pole are lines of abiding longitude, or meridians. The circles parallel to the equator are lines of constant latitude, or parallels. The graticule shows the latitude and longitude of points on the surface. In this instance meridians are spaced at half-dozen° intervals and parallels at iv° intervals.

In geography, latitude is a geographic coordinate that specifies the northward–south position of a signal on the Earth's surface. Breadth is an bending (defined below) which ranges from 0° at the Equator to 90° (Northward or Southward) at the poles. Lines of constant latitude, or parallels, run east–westward as circles parallel to the equator. Latitude is used together with longitude to specify the precise location of features on the surface of the World. On its own, the term breadth should be taken to be the geodetic latitude as divers below. Briefly, geodetic breadth at a point is the angle formed by the vector perpendicular (or normal) to the ellipsoidal surface from that point, and the equatorial plane. Also divers are half dozen auxiliary latitudes that are used in special applications.

Background [edit]

Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean body of water level over the oceans and its continuation nether the country masses. The second step is to estimate the geoid by a mathematically simpler reference surface. The simplest choice for the reference surface is a sphere, but the geoid is more accurately modeled by an ellipsoid. The definitions of latitude and longitude on such reference surfaces are detailed in the post-obit sections. Lines of constant breadth and longitude together constitute a graticule on the reference surface. The latitude of a betoken on the actual surface is that of the corresponding point on the reference surface, the correspondence beingness along the normal to the reference surface, which passes through the betoken on the physical surface. Latitude and longitude together with some specification of acme establish a geographic coordinate arrangement as divers in the specification of the ISO 19111 standard.^[1]

Since there are many different reference ellipsoids, the precise latitude of a feature on the surface is not unique: this is stressed in the ISO standard which states that "without the full specification of the coordinate reference system, coordinates (that is breadth and longitude) are ambiguous at best and meaningless at worst". This is of slap-up importance in accurate applications, such as a Global Positioning System (GPS), but in common usage, where loftier accurateness is not required, the reference ellipsoid is non usually stated.

In English texts, the latitude angle, defined below, is usually denoted by the Greek lower-case alphabetic character phi ( $ϕ$ or $φ$ ). It is measured in degrees, minutes and seconds or decimal degrees, northward or south of the equator. For navigational purposes positions are given in degrees and decimal minutes. For case, The Needles lighthouse is at l°39.734′ N 001°35.500′ W.^[ii]

This article relates to coordinate systems for the Globe: it may be adapted to cover the Moon, planets and other celestial objects (planetographic latitude).

For a cursory history run across History of latitude.

Decision [edit]

In angelic navigation, latitude is adamant with the superlative altitude method. More precise measurement of latitude requires an understanding of the gravitational field of the Earth, either to fix theodolites or to make up one's mind GPS satellite orbits. The study of the figure of the Earth together with its gravitational field is the science of geodesy.

Breadth on the sphere [edit]

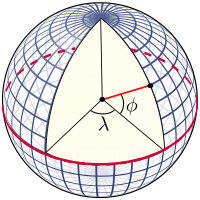
A perspective view of the Earth showing how breadth ( $\phi$ ) and longitude ( $\lambda$ ) are defined on a spherical model. The graticule spacing is 10 degrees.

The graticule on the sphere [edit]

The graticule is formed by the lines of abiding latitude and constant longitude, which are constructed with reference to the rotation centrality of the World. The primary reference points are the poles where the axis of rotation of the Earth intersects the reference surface. Planes which contain the rotation centrality intersect the surface at the meridians; and the angle betwixt any one meridian plane and that through Greenwich (the Prime number Meridian) defines the longitude: meridians are lines of abiding longitude. The airplane through the centre of the Earth and perpendicular to the rotation axis intersects the surface at a smashing circumvolve called the Equator. Planes parallel to the equatorial plane intersect the surface in circles of abiding latitude; these are the parallels. The Equator has a latitude of 0°, the North Pole has a latitude of ninety° Due north (written 90° N or +90°), and the S Pole has a breadth of xc° South (written 90° S or −90°). The breadth of an arbitrary bespeak is the angle between the equatorial plane and the normal to the surface at that indicate: the normal to the surface of the sphere is along the radius vector.

The latitude, equally divers in this fashion for the sphere, is often termed the spherical latitude, to avoid ambivalence with the geodetic breadth and the auxiliary latitudes divers in subsequent sections of this article.

Named latitudes on the World [edit]

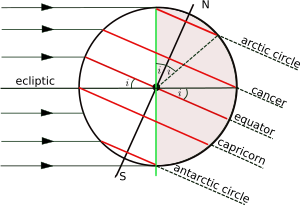
The orientation of the World at the December solstice.

Likewise the equator, four other parallels are of significance:

The plane of the Earth'south orbit about the Sun is chosen the ecliptic, and the airplane perpendicular to the rotation centrality of the Earth is the equatorial plane. The bending between the ecliptic and the equatorial plane is called variously the axial tilt, the obliquity, or the inclination of the ecliptic, and it is conventionally denoted by $i$ . The latitude of the tropical circles is equal to $i$ and the breadth of the polar circles is its complement (90° - i). The centrality of rotation varies slowly over time and the values given here are those for the electric current epoch. The fourth dimension variation is discussed more fully in the article on axial tilt.^[a]

The figure shows the geometry of a cantankerous-department of the aeroplane perpendicular to the ecliptic and through the centres of the World and the Sunday at the December solstice when the Dominicus is overhead at some indicate of the Tropic of Capricorn. The south polar latitudes below the Antarctic Circle are in daylight, whilst the north polar latitudes above the Chill Circle are in night. The state of affairs is reversed at the June solstice, when the Sun is overhead at the Tropic of Cancer. Only at latitudes in between the two tropics is it possible for the Lord's day to be directly overhead (at the zenith).

On map projections at that place is no universal dominion as to how meridians and parallels should appear. The examples beneath show the named parallels (every bit ruddy lines) on the commonly used Mercator project and the Transverse Mercator projection. On the former the parallels are horizontal and the meridians are vertical, whereas on the latter in that location is no exact relationship of parallels and meridians with horizontal and vertical: both are complicated curves.

	Normal Mercator		Transverse Mercator
		\

Latitude on the ellipsoid [edit]

Ellipsoids [edit]

In 1687 Isaac Newton published the Philosophiæ Naturalis Principia Mathematica, in which he proved that a rotating self-gravitating fluid body in equilibrium takes the form of an oblate ellipsoid.^[3] (This article uses the term ellipsoid in preference to the older term spheroid.) Newton'southward consequence was confirmed by geodetic measurements in the 18th century. (See Meridian arc.) An oblate ellipsoid is the 3-dimensional surface generated by the rotation of an ellipse about its shorter centrality (pocket-size centrality). "Oblate ellipsoid of revolution" is abbreviated to 'ellipsoid' in the remainder of this commodity. (Ellipsoids which do not have an axis of symmetry are termed triaxial.)

Many different reference ellipsoids have been used in the history of geodesy. In pre-satellite days they were devised to give a adept fit to the geoid over the limited area of a survey simply, with the advent of GPS, it has get natural to use reference ellipsoids (such every bit WGS84) with middle at the centre of mass of the Earth and minor axis aligned to the rotation centrality of the Earth. These geocentric ellipsoids are usually within 100 thousand (330 ft) of the geoid. Since latitude is defined with respect to an ellipsoid, the position of a given point is different on each ellipsoid: 1 cannot exactly specify the breadth and longitude of a geographical feature without specifying the ellipsoid used. Many maps maintained by national agencies are based on older ellipsoids, so one must know how the latitude and longitude values are transformed from one ellipsoid to another. GPS handsets include software to carry out datum transformations which link WGS84 to the local reference ellipsoid with its associated filigree.

The geometry of the ellipsoid [edit]

A sphere of radius a compressed along the z axis to form an oblate ellipsoid of revolution.

The shape of an ellipsoid of revolution is determined by the shape of the ellipse which is rotated almost its minor (shorter) axis. 2 parameters are required. Ane is invariably the equatorial radius, which is the semi-major axis, $a$ . The other parameter is unremarkably (ane) the polar radius or semi-minor axis, $b$ ; or (ii) the (commencement) flattening, $f$ ; or (three) the eccentricity, $due east$ . These parameters are not contained: they are related by

f={\frac {a-b}{a}},\qquad e^{2}=2f-f^{2},\qquad b=a(1-f)=a{\sqrt {1-east^{two}}}\,.

Many other parameters (run across ellipse, ellipsoid) appear in the report of geodesy, geophysics and map projections but they tin can all be expressed in terms of i or ii members of the set $a$ , $b$ , $f$ and $due east$ . Both $f$ and $due east$ are small and often appear in series expansions in calculations; they are of the order one / 298 and 0.0818 respectively. Values for a number of ellipsoids are given in Figure of the Earth. Reference ellipsoids are usually defined by the semi-major axis and the inverse flattening, $1 / f$ . For case, the defining values for the WGS84 ellipsoid, used by all GPS devices, are^[4]

$a$ (equatorial radius): vi378 137.0 m exactly
$1 / f$ (inverse flattening): 298.257223 563 exactly

from which are derived

$b$ (polar radius): half dozen356 752.31425 m
$e 2$ (eccentricity squared): 0.006694 379 990 14

The departure betwixt the semi-major and semi-minor axes is about 21 km (13 miles) and as fraction of the semi-major axis it equals the flattening; on a figurer monitor the ellipsoid could be sized equally 300 by 299 pixels. This would barely be distinguishable from a 300-by-300-pixel sphere, and so illustrations unremarkably exaggerate the flattening.

Geodetic and geocentric latitudes [edit]

The definition of geodetic latitude ( $\phi$ ) and longitude ( $\lambda$ ) on an ellipsoid. The normal to the surface does not pass through the heart, except at the equator and at the poles.

The graticule on the ellipsoid is constructed in exactly the aforementioned way as on the sphere. The normal at a indicate on the surface of an ellipsoid does not pass through the centre, except for points on the equator or at the poles, but the definition of breadth remains unchanged as the angle betwixt the normal and the equatorial airplane. The terminology for latitude must be made more precise past distinguishing:

Geodetic latitude: the bending between the normal and the equatorial plane. The standard notation in English publications is $ϕ$ . This is the definition causeless when the word latitude is used without qualification. The definition must exist accompanied with a specification of the ellipsoid.
Geocentric latitude (also known as spherical latitude, after the 3D polar bending): the angle betwixt the radius (from centre to the signal on the surface) and the equatorial airplane. (Figure beneath). In that location is no standard note: examples from various texts include $θ$ , $ψ$ , $q$ , $ϕ'$ , $ϕ c$ , $ϕ yard$ . This article uses $θ$ .

Geographic breadth must be used with care, every bit some authors use it as a synonym for geodetic latitude whilst others use it equally an alternative to the astronomical breadth. "Breadth" (unqualified) should normally refer to the geodetic latitude.

The importance of specifying the reference datum may be illustrated past a uncomplicated example. On the reference ellipsoid for WGS84, the center of the Eiffel Tower has a geodetic latitude of 48° 51′ 29″ N, or 48.8583° N and longitude of ii° 17′ 40″ Due east or 2.2944°E. The same coordinates on the datum ED50 define a point on the ground which is 140 metres (460 anxiety) distant from the tower.^{[ commendation needed ]} A web search may produce several dissimilar values for the latitude of the tower; the reference ellipsoid is rarely specified.

Height altitude [edit]

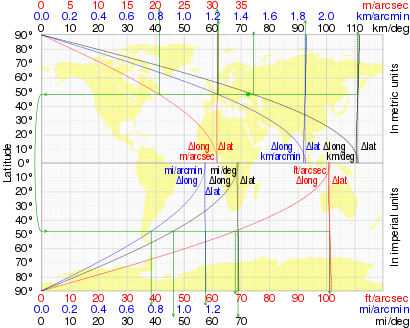
The length of a degree of latitude depends on the figure of the Earth causeless.

Meridian distance on the sphere [edit]

On the sphere the normal passes through the middle and the latitude ( $ϕ$ ) is therefore equal to the angle subtended at the heart by the pinnacle arc from the equator to the point concerned. If the elevation altitude is denoted by $thousand (ϕ)$ then

m(\phi )={\frac {\pi }{180^{\circ }}}R\phi _{\mathrm {degrees} }=R\phi _{\mathrm {radians} }

where $R$ denotes the mean radius of the Earth. $R$ is equal to 6,371 km or 3,959 miles. No higher accuracy is appropriate for $R$ since higher-precision results necessitate an ellipsoid model. With this value for $R$ the elevation length of 1 degree of latitude on the sphere is 111.2 km (69.1 statute miles) (60.0 nautical miles). The length of 1 minute of breadth is one.853 km (one.151 statute miles) (ane.00 nautical miles), while the length of 1 second of latitude is 30.eight m or 101 feet (see nautical mile).

Summit altitude on the ellipsoid [edit]

In Meridian arc and standard texts^[5] ^[6] ^[vii] it is shown that the distance along a meridian from breadth $ϕ$ to the equator is given by ( $ϕ$ in radians)

m(\phi )=\int _{0}^{\phi }1000(\phi ')\,d\phi '=a\left(i-e^{2}\correct)\int _{0}^{\phi }\left(ane-east^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '

where $K (ϕ)$ is the meridional radius of curvature.

The quarter top altitude from the equator to the pole is

m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,

For WGS84 this distance is ten001.965729 km.

The evaluation of the summit distance integral is central to many studies in geodesy and map projection. It can be evaluated by expanding the integral by the binomial series and integrating term past term: come across Meridian arc for details. The length of the superlative arc between ii given latitudes is given past replacing the limits of the integral by the latitudes concerned. The length of a small meridian arc is given by^[6] ^[7]

\delta m(\phi )=M(\phi )\,\delta \phi =a\left(i-due east^{2}\right)\left(1-e^{2}\sin ^{2}\phi \right)^{-{\frac {three}{2}}}\,\delta \phi

$\phi$	$Δ 1 lat$	$Δ 1 long$
0°	110.574 km	111.320 km
fifteen°	110.649 km	107.550 km
30°	110.852 km	96.486 km
45°	111.132 km	78.847 km
threescore°	111.412 km	55.800 km
75°	111.618 km	28.902 km
ninety°	111.694 km	0.000 km

When the latitude difference is 1 degree, corresponding to $π$ / 180 radians, the arc distance is about

\Delta _{\text{lat}}^{1}={\frac {\pi a\left(1-due east^{two}\right)}{180^{\circ }\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {iii}{2}}}}

The distance in metres (correct to 0.01 metre) between latitudes $\phi$ − 0.5 degrees and $\phi$ + 0.five degrees on the WGS84 spheroid is

\Delta _{\text{lat}}^{ane}=111\,132.954-559.822\cos 2\phi +1.175\cos 4\phi

The variation of this distance with latitude (on WGS84) is shown in the table along with the length of a degree of longitude (east–west altitude):

\Delta _{\text{long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {i-e^{two}\sin ^{2}\phi }}}}\,

A calculator for whatsoever breadth is provided by the U.Southward. Government'south National Geospatial-Intelligence Agency (NGA).^[8]

The following graph illustrates the variation of both a degree of latitude and a caste of longitude with latitude.

The definition of geodetic latitude ( $ϕ$ ) and geocentric latitude ( $θ$ ).

Auxiliary latitudes [edit]

There are six auxiliary latitudes that accept applications to special problems in geodesy, geophysics and the theory of map projections:

Geocentric latitude
Parametric (or reduced) latitude
Rectifying latitude
Authalic latitude
Conformal latitude
Isometric latitude

The definitions given in this department all chronicle to locations on the reference ellipsoid but the first ii auxiliary latitudes, like the geodetic breadth, can exist extended to ascertain a iii-dimensional geographic coordinate system every bit discussed beneath. The remaining latitudes are not used in this style; they are used only every bit intermediate constructs in map projections of the reference ellipsoid to the airplane or in calculations of geodesics on the ellipsoid. Their numerical values are non of interest. For example, no one would need to calculate the authalic latitude of the Eiffel Tower.

The expressions beneath requite the auxiliary latitudes in terms of the geodetic breadth, the semi-major axis, $a$ , and the eccentricity, $eastward$ . (For inverses see below.) The forms given are, apart from notational variants, those in the standard reference for map projections, namely "Map projections: a working manual" past J. P. Snyder.^[9] Derivations of these expressions may be found in Adams^[10] and online publications by Osborne^[6] and Rapp.^[7]

Geocentric latitude [edit]

The definition of geodetic latitude ( $ϕ$ ) and geocentric breadth ( $θ$ ).

The geocentric breadth is the angle between the equatorial plane and the radius from the centre to a point of interest.

When the indicate is on the surface of the ellipsoid, the relation between the geocentric latitude ( $θ$ ) and the geodetic breadth ( $ϕ$ ) is:

\theta (\phi )=\tan ^{-1}\left(\left(ane-due east^{two}\right)\tan \phi \right)=\tan ^{-1}\left((1-f)^{ii}\tan \phi \right)\,.

For points non on the surface of the ellipsoid, the relationship involves additionally the oblong height h:

\theta (\phi ,h)=\tan ^{-1}\left({\frac {N(i-f)^{2}+h}{N+h}}\tan \phi \right)

The geodetic and geocentric latitudes are equal at the equator and at the poles but at other latitudes they differ by a few minutes of arc. Taking the value of the squared eccentricity as 0.0067 (it depends on the choice of ellipsoid) the maximum difference of $\phi {-}\theta$ may be shown to be about 11.5 minutes of arc at a geodetic latitude of approximately 45° 6′.^[b]

Parametric latitude (or reduced latitude) [edit]

Definition of the parametric latitude ( $β$ ) on the ellipsoid.

The parametric breadth or reduced latitude, $β$ , is defined by the radius drawn from the centre of the ellipsoid to that point $Q$ on the surrounding sphere (of radius $a$ ) which is the projection parallel to the World's axis of a point $P$ on the ellipsoid at latitude $ϕ$ . Information technology was introduced by Legendre^[11] and Bessel^[12] who solved problems for geodesics on the ellipsoid by transforming them to an equivalent problem for spherical geodesics by using this smaller latitude. Bessel's notation, $u (ϕ)$ , is also used in the current literature. The parametric breadth is related to the geodetic breadth by:^[6] ^[7]

\beta (\phi )=\tan ^{-i}\left({\sqrt {1-e^{ii}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)

The alternative name arises from the parameterization of the equation of the ellipse describing a tiptop section. In terms of Cartesian coordinates $p$ , the altitude from the minor axis, and $z$ , the distance above the equatorial plane, the equation of the ellipse is:

{\frac {p^{two}}{a^{two}}}+{\frac {z^{2}}{b^{2}}}=1\,.

The Cartesian coordinates of the indicate are parameterized by

p=a\cos \beta \,,\qquad z=b\sin \beta \,;

Cayley suggested the term parametric latitude because of the form of these equations.^[13]

The parametric breadth is not used in the theory of map projections. Its about important awarding is in the theory of ellipsoid geodesics, (Vincenty, Karney^[xiv]).

Rectifying latitude [edit]

The rectifying latitude, $μ$ , is the meridian distance scaled so that its value at the poles is equal to xc degrees or $π$ / 2 radians:

\mu (\phi )={\frac {\pi }{2}}{\frac {m(\phi )}{m_{\mathrm {p} }}}

where the superlative distance from the equator to a latitude $ϕ$ is (see Tiptop arc)

m(\phi )=a\left(one-e^{2}\right)\int _{0}^{\phi }\left(1-due east^{2}\sin ^{2}\phi '\correct)^{-{\frac {iii}{2}}}\,d\phi '\,,

and the length of the meridian quadrant from the equator to the pole (the polar altitude) is

m_{\mathrm {p} }=grand\left({\frac {\pi }{2}}\correct)\,.

Using the rectifying latitude to define a latitude on a sphere of radius

R={\frac {2m_{\mathrm {p} }}{\pi }}

defines a projection from the ellipsoid to the sphere such that all meridians accept true length and uniform scale. The sphere may then exist projected to the airplane with an equirectangular project to give a double project from the ellipsoid to the aeroplane such that all meridians have true length and compatible top scale. An example of the utilise of the rectifying breadth is the equidistant conic project. (Snyder, Department 16).^[9] The rectifying latitude is also of great importance in the structure of the Transverse Mercator project.

Authalic latitude [edit]

The authalic breadth (after the Greek for "same surface area"), $ξ$ , gives an area-preserving transformation to a sphere.

\xi (\phi )=\sin ^{-ane}\left({\frac {q(\phi )}{q_{\mathrm {p} }}}\right)

where

{\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{i-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{two}}{2e}}\ln \left({\frac {i-east\sin \phi }{1+e\sin \phi }}\correct)\\[2pt]&={\frac {\left(1-east^{two}\right)\sin \phi }{1-e^{2}\sin ^{two}\phi }}+{\frac {1-e^{2}}{due east}}\tanh ^{-1}(due east\sin \phi )\end{aligned}}

and

{\begin{aligned}q_{\mathrm {p} }=q\left({\frac {\pi }{2}}\right)&=1-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-east}{i+e}}\correct)\\&=1+{\frac {1-eastward^{2}}{e}}\tanh ^{-1}e\stop{aligned}}

and the radius of the sphere is taken equally

R_{q}=a{\sqrt {\frac {q_{\mathrm {p} }}{2}}}\,.

An example of the use of the authalic breadth is the Albers equal-area conic projection.^[ix] ^: §14

Conformal latitude [edit]

The conformal latitude, $χ$ , gives an angle-preserving (conformal) transformation to the sphere.

{\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {one+\sin \phi }{1-\sin \phi }}\right)\left({\frac {1-e\sin \phi }{1+due east\sin \phi }}\right)^{e}\right]^{\frac {1}{2}}-{\frac {\pi }{ii}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{iv}}\right)\left({\frac {one-e\sin \phi }{1+due east\sin \phi }}\right)^{\frac {e}{2}}\right]-{\frac {\pi }{two}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-one}(\tan \phi )-east\tanh ^{-i}(e\sin \phi )\right)\right]\\&=\operatorname {gd} \left[\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-i}(east\sin \phi )\right]\end{aligned}}

where $gd(x)$ is the Gudermannian function. (Come across also Mercator projection.)

The conformal latitude defines a transformation from the ellipsoid to a sphere of arbitrary radius such that the angle of intersection between any two lines on the ellipsoid is the aforementioned as the corresponding angle on the sphere (so that the shape of pocket-sized elements is well preserved). A farther conformal transformation from the sphere to the plane gives a conformal double project from the ellipsoid to the aeroplane. This is not the merely mode of generating such a conformal projection. For example, the 'verbal' version of the Transverse Mercator projection on the ellipsoid is non a double project. (It does, however, involve a generalisation of the conformal latitude to the circuitous aeroplane).

Isometric latitude [edit]

The isometric latitude, $ψ$ , is used in the development of the oblong versions of the normal Mercator project and the Transverse Mercator projection. The proper noun "isometric" arises from the fact that at whatsoever betoken on the ellipsoid equal increments of $ψ$ and longitude $λ$ give rise to equal altitude displacements along the meridians and parallels respectively. The graticule defined past the lines of abiding $ψ$ and constant $λ$ , divides the surface of the ellipsoid into a mesh of squares (of varying size). The isometric latitude is zero at the equator just chop-chop diverges from the geodetic latitude, tending to infinity at the poles. The conventional notation is given in Snyder (page 15):^[9]

{\brainstorm{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}}\right)\right]+{\frac {due east}{ii}}\ln \left[{\frac {i-e\sin \phi }{1+e\sin \phi }}\right]\\&=\sinh ^{-1}(\tan \phi )-due east\tanh ^{-1}(eastward\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-ane}(eastward\sin \phi ).\end{aligned}}

For the normal Mercator projection (on the ellipsoid) this function defines the spacing of the parallels: if the length of the equator on the projection is $E$ (units of length or pixels) and then the distance, $y$ , of a parallel of latitude $ϕ$ from the equator is

y(\phi )={\frac {Eastward}{2\pi }}\psi (\phi )\,.

The isometric breadth $ψ$ is closely related to the conformal latitude $χ$ :

\psi (\phi )=\operatorname {gd} ^{-1}\chi (\phi )\,.

Inverse formulae and series [edit]

The formulae in the previous sections give the auxiliary latitude in terms of the geodetic latitude. The expressions for the geocentric and parametric latitudes may be inverted directly but this is impossible in the four remaining cases: the rectifying, authalic, conformal, and isometric latitudes. In that location are ii methods of proceeding.

The first is a numerical inversion of the defining equation for each and every detail value of the auxiliary latitude. The methods available are stock-still-point iteration and Newton–Raphson root finding.
- When converting from isometric or conformal to geodetic, two iterations of Newton-Raphson gives double precision accuracy.^[15]
The other, more useful, approach is to express the auxiliary latitude as a series in terms of the geodetic latitude and and then invert the serial by the method of Lagrange reversion. Such series are presented by Adams who uses Taylor series expansions and gives coefficients in terms of the eccentricity.^[10] Osborne derives serial to arbitrary order by using the computer algebra package Maxima and expresses the coefficients in terms of both eccentricity and flattening. The series method is not applicable to the isometric latitude and 1 must discover the conformal latitude in an intermediate step.^{[half dozen]}

Numerical comparison of auxiliary latitudes [edit]

The plot to the right shows the difference between the geodetic latitude and the auxiliary latitudes other than the isometric latitude (which diverges to infinity at the poles) for the case of the WGS84 ellipsoid. The differences shown on the plot are in arc minutes. In the Northern hemisphere (positive latitudes), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ; in the Southern hemisphere (negative latitudes), the inequalities are reversed, with equality at the equator and the poles. Although the graph appears symmetric nearly 45°, the minima of the curves actually lie between 45° two′ and 45° 6′. Some representative data points are given in the tabular array beneath. The conformal and geocentric latitudes are nearly indistinguishable, a fact that was exploited in the days of hand calculators to expedite the construction of map projections.^[nine] ^: 108

To starting time lodge in the flattening f, the auxiliary latitudes can be expressed as ζ = ϕ − Cf sin twoϕ where the constant C takes on the values [ 1⁄2 , 2⁄3 , 3⁄4 , 1, 1] for ζ = [β, ξ, μ, χ, θ].

Approximate divergence from geodetic latitude ( $ϕ$ )
$ϕ$	Parametric $β - ϕ$	Authalic $ξ - ϕ$	Rectifying $μ - ϕ$	Conformal $χ - ϕ$	Geocentric $θ - ϕ$
0°	0.00′	0.00′	0.00′	0.00′	0.00′
15°	−2.88′	−3.84′	−4.32′	−5.76′	−v.76′
thirty°	−v.00′	−6.66′	−seven.49′	−9.98′	−9.98′
45°	−5.77′	−7.lxx′	−viii.66′	−11.54′	−11.55′
60°	−five.00′	−6.67′	−seven.51′	−10.01′	−10.02′
75°	−2.89′	−iii.86′	−4.34′	−5.78′	−5.79′
90°	0.00′	0.00′	0.00′	0.00′	0.00′

Latitude and coordinate systems [edit]

The geodetic latitude, or any of the auxiliary latitudes defined on the reference ellipsoid, constitutes with longitude a two-dimensional coordinate system on that ellipsoid. To define the position of an capricious point information technology is necessary to extend such a coordinate arrangement into three dimensions. Three latitudes are used in this way: the geodetic, geocentric and parametric latitudes are used in geodetic coordinates, spherical polar coordinates and ellipsoidal coordinates respectively.

Geodetic coordinates [edit]

Geodetic coordinates $P(ɸ, λ, h)$

At an arbitrary point $P$ consider the line $PN$ which is normal to the reference ellipsoid. The geodetic coordinates $P(ɸ, λ, h)$ are the latitude and longitude of the bespeak $N$ on the ellipsoid and the altitude $PN$ . This height differs from the peak above the geoid or a reference superlative such equally that above mean sea level at a specified location. The direction of $PN$ will also differ from the management of a vertical plumb line. The relation of these different heights requires knowledge of the shape of the geoid and also the gravity field of the Globe.

Spherical polar coordinates [edit]

Geocentric coordinate related to spherical polar coordinates $P(r, θ', λ)$

The geocentric breadth $θ$ is the complement of the polar bending or colatitude $θ'$ in conventional spherical polar coordinates in which the coordinates of a betoken are $P(r, θ', λ)$ where $r$ is the distance of $P$ from the centre $O$ , $θ'$ is the bending between the radius vector and the polar axis and $λ$ is longitude. Since the normal at a full general point on the ellipsoid does not pass through the eye it is clear that points $P'$ on the normal, which all have the aforementioned geodetic latitude, will have differing geocentric latitudes. Spherical polar coordinate systems are used in the assay of the gravity field.

Oblong-harmonic coordinates [edit]

Ellipsoidal coordinates $P(u, β, λ)$

The parametric latitude can also be extended to a three-dimensional coordinate organisation. For a point $P$ non on the reference ellipsoid (semi-axes $OA$ and $OB$ ) construct an auxiliary ellipsoid which is confocal (same foci $F$ , $F'$ ) with the reference ellipsoid: the necessary condition is that the production $ae$ of semi-major axis and eccentricity is the aforementioned for both ellipsoids. Let $u$ be the semi-minor axis ( $OD$ ) of the auxiliary ellipsoid. Further let $β$ be the parametric latitude of $P$ on the auxiliary ellipsoid. The set $(u, β, λ)$ define the ellipsoidal-harmonic coordinates ^[16] or simply ellipsoidal coordinates ^[5] ^: §iv.2.2 (although that term is also used to refer to geodetic coordinate). These coordinates are the natural choice in models of the gravity field for a rotating ellipsoidal body. The above applies to a biaxial ellipsoid (a spheroid, as in oblate spheroidal coordinates); for a generalization, run across triaxial ellipsoidal coordinates.

Coordinate conversions [edit]

The relations between the to a higher place coordinate systems, and as well Cartesian coordinates are not presented here. The transformation between geodetic and Cartesian coordinates may be found in Geographic coordinate conversion. The relation of Cartesian and spherical polars is given in Spherical coordinate organisation. The relation of Cartesian and oblong coordinates is discussed in Torge.^[five]

Astronomical breadth [edit]

Astronomical latitude ( $Φ$ ) is the angle between the equatorial aeroplane and the true vertical direction at a point on the surface. The truthful vertical, the direction of a plumb line, is also the gravity direction (the resultant of the gravitational dispatch (mass-based) and the centrifugal acceleration) at that latitude.^[v] Astronomic latitude is calculated from angles measured between the zenith and stars whose declination is accurately known.

In full general the true vertical at a point on the surface does not exactly coincide with either the normal to the reference ellipsoid or the normal to the geoid. The bending between the astronomic and geodetic normals is called vertical deflection and is usually a few seconds of arc merely it is of import in geodesy.^[5] ^[17] The reason why it differs from the normal to the geoid is, because the geoid is an idealized, theoretical shape "at mean sea level". Points on the real surface of the world are usually above or below this arcadian geoid surface and hither the true vertical can vary slightly. Too, the true vertical at a indicate at a specific fourth dimension is influenced by tidal forces, which the theoretical geoid averages out.

Astronomical latitude is non to be dislocated with declination, the coordinate astronomers apply in a like manner to specify the angular position of stars northward/south of the celestial equator (meet equatorial coordinates), nor with ecliptic latitude, the coordinate that astronomers use to specify the angular position of stars due north/south of the ecliptic (see ecliptic coordinates).

References [edit]

Footnotes [edit]

^ The value of this bending today is 23°26′11.0″ (or 23.4364°). This effigy is provided by Template:Circle of latitude.
^ An simple calculation involves differentiation to find the maximum deviation of the geodetic and geocentric latitudes.

Citations [edit]

^ "ISO 19111 Geographic information — Referencing by coordinates". ISO. 2021-06-01. Retrieved 2022-01-sixteen .
^ The Corporation of Trinity House (10 January 2020). "one/2020 Needles Lighthouse". Notices to Mariners. Retrieved 24 May 2020.
^ Newton, Isaac. "Book 3 Proposition Nineteen Problem III". Philosophiæ Naturalis Principia Mathematica. Translated past Motte, Andrew. p. 407.
^ National Imagery and Mapping Agency (23 June 2004). "Department of Defense Earth Geodetic System 1984" (PDF). National Imagery and Mapping Agency. p. iii-i. TR8350.2. Retrieved 25 Apr 2020.
^ ^a ^b ^c ^d ^e Torge, W. (2001). Geodesy (tertiary ed.). De Gruyter. ISBN3-eleven-017072-8.
^ ^a ^b ^c ^d ^e Osborne, Peter (2013). "Chapters 5,6". The Mercator Projections. doi:10.5281/zenodo.35392. for LaTeX code and figures.
^ ^a ^b ^c ^d Rapp, Richard H. (1991). "Affiliate 3". Geometric Geodesy, Part I. Columbus, OH: Dept. of Geodetic Science and Surveying, Ohio State Univ. hdl:1811/24333.
^ "Length of degree computer". National Geospatial-Intelligence Agency. Archived from the original on 2013-01-28. Retrieved 2011-02-08 .
^ ^a ^b ^c ^d ^e Snyder, John P. (1987). Map Projections: A Working Transmission. U.S. Geological Survey Professional Paper 1395. Washington, DC: United states Government Printing Office. Archived from the original on 2008-05-16. Retrieved 2017-09-02 .
^ ^a ^b Adams, Oscar S. (1921). Breadth Developments Continued With Geodesy and Cartography (with tables, including a table for Lambert equal expanse meridional projection (PDF). Special Publication No. 67. US Coast and Geodetic Survey. (Note: Adams uses the classification isometric latitude for the conformal latitude of this article (and throughout the modern literature).)
^ Legendre, A. M. (1806). "Analyse des triangles tracés sur la surface d'un sphéroïde". Mém. Inst. Nat. Fr. 1st semester: 130–161.
^ Bessel, F. Westward. (1825). "Über die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen". Astron. Nachr. four (86): 241–254. arXiv:0908.1824. Bibcode:2010AN....331..852K. doi:10.1002/asna.201011352. S2CID 118760590.
Translation: Karney, C. F. F.; Deakin, R. Eastward. (2010). "The calculation of longitude and latitude from geodesic measurements". Astron. Nachr. 331 (8): 852–861. arXiv:0908.1824. Bibcode:1825AN......4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
^ Cayley, A. (1870). "On the geodesic lines on an oblate spheroid". Phil. Mag. forty (4th ser): 329–340. doi:10.1080/14786447008640411.
^ Karney, C. F. F. (2013). "Algorithms for geodesics". Periodical of Geodesy. 87 (1): 43–55. arXiv:1109.4448. Bibcode:2013JGeod..87...43K. doi:ten.1007/s00190-012-0578-z. S2CID 119310141.
^ Karney, Charles F. F. (Baronial 2011). "Transverse Mercator with an accuracy of a few nanometers". Journal of Geodesy. 85 (8): 475–485. arXiv:1002.1417. Bibcode:2011JGeod..85..475K. doi:ten.1007/s00190-011-0445-3. S2CID 118619524.
^ Holfmann-Wellenfor & Moritz (2006) Physical Geodesy, p.240, eq. (6-6) to (6-10).
^ Hofmann-Wellenhof, B.; Moritz, H. (2006). Physical Geodesy (2nd ed.). ISBN3-211-33544-7.

External links [edit]

GEONets Names Server, access to the National Geospatial-Intelligence Agency's (NGA) database of foreign geographic feature names.
Resources for determining your latitude and longitude
Convert decimal degrees into degrees, minutes, seconds - Info about decimal to sexagesimal conversion
Convert decimal degrees into degrees, minutes, seconds
Distance calculation based on latitude and longitude - JavaScript version
16th Century Latitude Survey
Determination of Latitude by Francis Drake on the Coast of California in 1579

thorpedisser.blogspot.com

Source: https://en.wikipedia.org/wiki/Latitude